Задания ОЧ-2016: 8 класс индивидуальный тур

До VII Открытого чемпионата еще 3 месяца. Но команда организаторов предлагает тебе не терять время и начать готовиться к Чемпионату уже сейчас. Представляем вам задания 8 класса индивидуального тура.
Задача 1: Взвешенное решение.
У школьника Васи есть 9 внешне одинаковых монет, одна из которых фальшивая (она весит чуть меньше остальных). Мальчик очень любит конфеты и тратит все деньги только на них, его счастье прямо пропорционально числу купленных конфет. Однако он знает, что если он попробует расплатиться фальшивой монетой, то в его городе больше никогда никто не продаст ему конфеты, поэтому ему очень хочется узнать, какая из монет фальшивая.
- Помочь ему в этом может индивидуальный предприниматель Жора, у которого имеются два экземпляра внешне неразличимых чашечных весов, из которых одни неисправны (при любом взвешивании, в котором на чашах поровну монет, показывают равенство). Какие из весов неисправны, Жора не рассказывает. Вася может сделать сколько захочет взвешиваний, однако, каждое взвешивание у Жоры стоит одну настоящую монету (плата взимается после окончания всех взвешиваний, Вася не может взвешивать «в кредит»). Какое наибольшее количество конфет сможет гарантированно купить Вася, если цена одного килограмма конфет – одна монета?
- Недалеко от Жоры работает его конкурент, Константин, у которого есть одни исправно работающие чашечные весы. Какую наибольшую цену одного взвешивания может поставить Константин, чтобы Васе было выгоднее идти к нему, если при прочих равных Вася предпочтет иметь дело с честным Константином, а монеты можно разменивать на меньшие по ценности. (При выборе Вася руководствуется тем количеством взвешиваний, которое позволит гарантированно выявить фальшивку, потому что он пессимист.)
Решение:
- Пронумеруем монеты от 1 до 9. Для первого взвешивания положим на одну чашу монеты под номерами 1, 2, 3, 4 и на другую – с номерами 5, 6, 7, 8. Если монеты на одной чаше оказались легче другой, то данные весы исправны, фальшивая монета в этой четверке, и за два взвешивания на этих весах мы найдем фальшивку.
Если чаши при первом взвешивании остались в равновесии, то вторым взвешиванием кладем на чаши вторых весов монеты с номерами 1, 2, 3 и 5, 6, 7. Если в этот раз чаши оказались на разном уровне, то мы нашли хорошие весы и три монеты, среди которых фальшивая, за последнее взвешивание на них найдем фальшивую монету.
Если и во второй раз чаши находятся в равновесии, то возможна одна из двух ситуаций: первые весы неисправны, а фальшивая монета – одна из 4, 8, 9; вторые весы неисправны и 9 – фальшивка. Таким образом, если третьим взвешиванием положить на вторые весы монеты 4 и 8, то, в зависимости от исхода, достоверно определим фальшивую монету: если чаши в равновесии – фальшивая монета с номером 9, если одна перевешивает, то та, чаша с которой легче.
Докажем, что за два взвешивания точно определить нельзя, будем действовать от противного и рассмотрим варианты первого взвешивания:
- На чашах – по 4 монеты, на весах – неравновесие, тогда за оставшееся одно взвешивание не получится выявить фальшивую монету из 4 подозрительных.
- Если на чашах было меньше, чем по 4 монеты, но равновесие при первом взвешивании, то отложено больше одной монеты, и если проведем второе взвешивание на вторых весах (это необходимое условие для проверки весов), а они окажутся неисправными, то мы не сможем понять, какая из отложенных монет фальшивая.
Таким образом, Вася не сможет сделать меньше трех взвешиваний, то есть отдаст Жоре не меньше трех монет. Фальшивую монету Жора не возьмет, а значит Вася сможет купить не больше 5 кг конфет.
Ответ: 5 кг.
Примечание: допускается использование других путей решения или оформление с помощью графа последовательных событий.
- Из 9 монет на исправных весах определить фальшивую монету можно за 2 взвешивания: кладем на обе чаши по три монеты; если одна из чаш перевешивает, то фальшивая монета на чаше, оказавшейся легче; если чаши оказались в равновесии, то фальшивая – одна из трех оставшихся монет. Таким образом мы выбрали три монеты, среди которых есть фальшивая. Вторым взвешиванием кладем по одной монете на чаши из выбранной тройки, определяем, какая из них фальшивая аналогично алгоритму первого взвешивания.
За одно взвешивание определить фальшивую монету нельзя, так как, сколько бы монет мы ни положили на чаши в первом взвешивании, после него может остаться несколько монет, среди которых будет фальшивка (можно разобрать каждый случай: по 1, по 2, по 3, по 4 на каждой чаше в первое взвешивание). Жоре Вася отдаст 3 монеты, значит, чтобы мальчику выгодно было идти к Константину, цена одного взвешивания не должна превышать 1,5 монеты.
Ответ: 1,5 монеты.
Задача 2:
У выигравшего в лотерею 100.000 рублей учителя Николая Петровича есть два варианта распоряжения новоприобретенными деньгами – он может либо вложить их в дело своей жены, Натальи Сергеевны, чтобы расширить производство ее компании по изготовлению шляпок, либо положить деньги в Банк «Выгодный» в качестве вклада (комбинировать два этих варианта нельзя).
Банк «Выгодный» предлагает Николаю Петровичу очень выгодную процентную ставку – 50% годовых. (Процент начисляется в конце года на сумму, лежащую в банке на момент начисления, то есть с учётом предыдущих начислений.) Наталья Сергеевна уверена, что, если Николай Петрович инвестирует деньги в ее компанию, уже через 3 года она сможет вернуть ему эти деньги в тройном размере (за вычетом 9-процентного налога на прибыль с окончательной суммы).
Пытаясь решить, как лучше поступить, Николай Петрович внимательно вчитывается в договор на вклад с Банком «Выгодный» и видит пункт мелким шрифтом, говорящий о том, что, начиная со второго года, Банк «Выгодный» будет уменьшать процентную ставку на фиксированное (Х) количество процентных пунктов. Найдите максимальный X, при котором Николаю Петровичу будет выгодно отнести деньги в Банк, тем самым расстроив свою жену.
Решение:
- Вычислим, сколько денег Н. П. получит, если инвестирует выигрыш в компанию жены. Инвестиции вернут в тройном размере, за вычетом 9 процентного налога на прибыль с окончательной суммы.
100.000 * 3 = 300.000 р – прибыль до налога
300.000 * (1,00 – 0,09) = 273.000 р – столько Н. П. получит денег, если отдаст их жене
- Если Н. П. отнесет деньги в Банк «Выгодный», то
- к концу первого года он будет иметь 100.000 * (1 + 0,5) = 150.000 р
- к концу второго года (когда Банк уменьшит ставку на X %)
150.000 + 150.000 * (0,5 – X) р
- к концу третьего года (ставка уменьшится еще на X %) на счету будет
150.000 + 150.000 * (0,5 – X) + [150.000 + 150.000 * (0,5 – X)]*(0,5 – 2X) р
- Теперь составим уравнение. Необходимо найти максимальный X, при котором будет выгодно отнести деньги в Банк. То есть
150.000 + 150.000 * (0,5 – X) + [150.000 + 150.000 * (0,5 – X)]*(0,5 – 2X) 273.000 Для удобства (и так как нам надо найти максимальный X) будем рассматривать равенство данного выражения.
150.000 + 150.000 * (0,5 – X) + [150.000 + 150.000 * (0,5 – X)]*(0,5 – 2X) = 273.000
150 + 150 * (0,5 – X) + (150 + 75 – 150X)*(0,5 – 2X) = 273
150 + 75 – 150X + (225 – 150X)*(0,5-2X) = 273
225 – 150X + 112,5 – 450X – 75X +300 – 273 = 0
300 — 675X + 64,5 = 0
– 2,25X +0,215 = 0
(X – 0,1) * (X – 2,15) = 0 (здесь можно воспользоваться формулой дискриминанта)
X=2,15 – корень не подходит
X=0,1 – ответ
Ответ: максимальный X, при котором Николаю Петровичу будет выгодно отнести деньги в Банк «Выгодный», равен 10 процентным пунктам.
Задача 3:
Предположим, что вы ежедневно совершаете поездки из дома на работу и обратно на легковом автомобиле по новой платной трассе, соединяющей Зеленоград и Москву. Базовый тариф за проезд по маршруту Зеленоград – Москва в утренний час пик (6:00 – 10:00) составляет 400 рублей. Базовый тариф за проезд по маршруту Москва – Зеленоград в вечерний час пик (16:00 – 22:00) составляет 350 рублей. (Оба тарифа указаны с учётом затрат на бензин.) Альтернатива «ехать по бесплатной дороге» вам глубоко противна, так как Ленинградское шоссе является чрезвычайно загруженным. Однако существует ещё альтернатива пользования электричкой.
Вы рассматриваете период из 10 недель по 5 рабочих дней в каждой, то есть 50 поездок туда и 50 поездок обратно. Стоимость пользования электричкой за это время составит 21300 рублей.
Для пользования платной дорогой вам предлагают следующую скидочную программу, стоимость которой оплачивается единовременно до начала использования:
| Первые 20 поездок | Следующие 10 поездок | Следующие 14 поездок | Следующие 6 поездок |
| Скидка 𝑥% | Скидка (𝑥+30)% | Скидка (𝑥+40)% | Скидка (𝑥+50)% |
Какой должна быть величина скидки на первые 20 поездок, чтобы вам было все равно, пользоваться ли платной дорогой со скидочной программой или совершать поездки на электричке?
Решение:
Составим таблицу платы за проезд по платной дороге:
| Без использования скидочной программы | С использованием скидочной программы | |
| Первые 20 поездок | ||
| Следующие 10 поездок | ||
| Следующие 14 поездок | ||
| Следующие 6 поездок | ||
| СУММА |
Тогда вам будет все равно, пользоваться ли платной дорогой со скидочной программой или совершать поездки на электричке, если:
Ответ: Скидка должна составлять 20%.
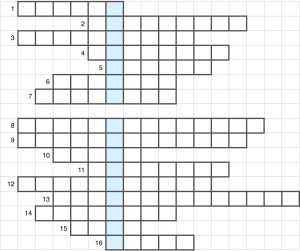
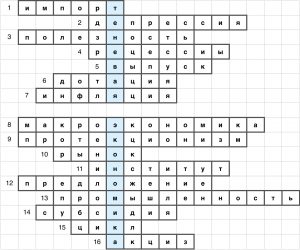
Задача 4
- Ввоз товаров, работ, услуг и т.п. на территорию страны из-за границы.
- Длительный спад совокупной экономической активности.
- Способность товара удовлетворять человеческую потребность.
- Краткосрочный спад производства в экономике, снижение темпов роста.
- Объём произведённых товаров и услуг.
- Безвозмездный трансферт, осуществляемый государством, с целью покрытия убытка предприятия.
- Устойчивый рост общего уровня цен в экономике.
- Раздел экономической науки, изучающий экономику страны или мира как единое целое.
- Экономическая политика, направленная на поддержку внутреннего производителя и его защиту от зарубежной конкуренции.
- Совокупность экономических отношений, базирующихся на обмене товарами и услугами между производителями и потребителями.
- Совокупность правила и механизма принуждения к исполнению этого правила.
- Готовность фирмы произвести определённое количество товара при заданных условиях.
- Совокупность предприятий, занятых производством орудий труда, добычей сырья, материалов, топлива, производством энергии и дальнейшей обработкой продуктов.
- Безвозмездная передача средств из государственного бюджета фирмам или потребителям, обычно с целью стимулирования производства конкретного товара.
- Периодическое колебание экономической активности.
- Косвенный налог, устанавливаемый на предметы массового потребления внутри страны.
Решение: