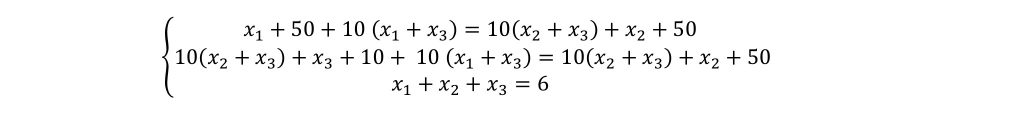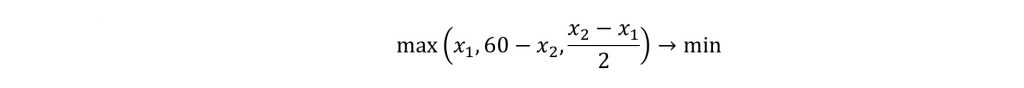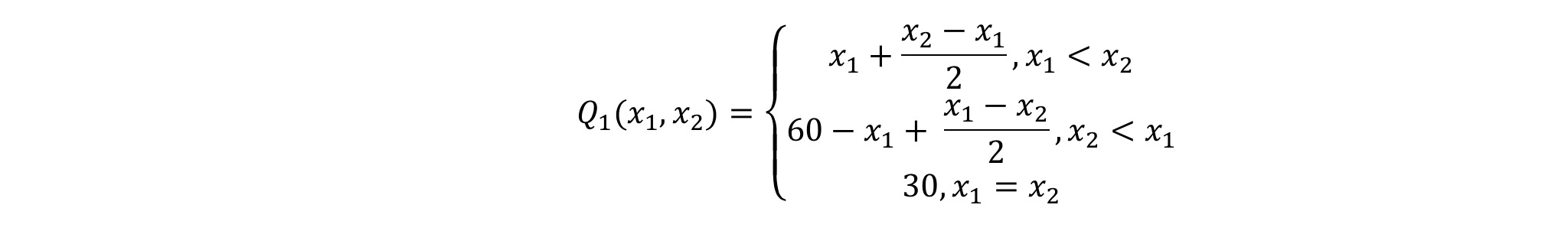Задания ОЧ-2016: 9 класс индивидуальный тур

Когда-то математики использовали громоздкое словесное описание уравнений. Но в XVI веке Франсуа Виет вводит символьные обозначения, и появляется возможность производить преобразования алгебраических выражений. Применив логику и достижения математической науки, вы обязательно справитесь с заданиями индивидуального этапа для 9 класса.

Задача 1

В некотором государстве есть Промзона, а также есть морской Порт, куда каждый день ездят 6 тысяч машин. Так сложилась жизнь, что из Промзоны в Порт можно попасть, если ехать либо через город Альфа, либо через город Бета. В зависимости от того, сколько машин едет по участку дороги (в этот день), время движения по ней составит T(c) минут, где c – загруженность дороги (в тыс. машин).

1. Считая, что каждый водитель знает о текущей дорожной обстановке, и предполагая, что он минимизирует время на проезд, определите равновесное время в пути.
2. Правительство решает улучшить дорожную ситуацию. Для этого оно строит дорогу (одностороннюю) из города Бета в город Альфа. Время движения по этой дороге составляет 
T(c) = c + 10. Определите, какое время необходимо будет затратить теперь для того, чтобы попасть из Промзоны в Порт. Дайте объяснение полученному ответу.
3. Предложите возможные способы для улучшения ситуации, полученной в предыдущем пункте.

Решение:

1. Есть два пути: через Альфу и через Бету. Водители минимизируют время в пути, следовательно, в равновесии время в пути по каждой из дорог будет одинаковым. (Иначе кто-то бы с более долгой дороги перешел на более быструю). Заметим, что наши пути эквивалентны. Поэтому по каждой дороге поедет ровно половина машин, то есть 3000. Время в пути составит 83 минуты.

Ответ: 83 минуты.

2. Аналогично предыдущему пункту, время в пути по каждому из маршрутов в равновесии будет одинаковым.

Теперь рассмотрим три маршрута:

• Промзона-Альфа-Порт (1й маршрут)
• Промзона-Бета-Порт (2й маршрут)
• Промзона-Альфа-Бета-Порт (3й маршрут)

Пусть X1 едет по 1му, X2 едет по 2му, X3 едет по 3му маршруту. Тогда получим систему уравнений:

Откуда X1 = X2 = X3 = 2 . Тогда время в пути (по каждому из маршрутов) составит 92 минуты, т.е. время в пути увеличилось.
Объяснение: новый маршрут позволяет миновать более загруженный участок с пропускной способностью T(c) = c + 50. Но, с другой стороны, он создает нагрузку на участки T(c) = 10c. Получается, что новый участок увеличивает загрузку на существовавшие участки дороги, что приводит к замедлению движения.

3. Возможные варианты:

• Закрыть новый участок дороги и вернуться к исходной ситуации.
• Ввести квоту на проезд. Т.е., например, пускать только по 500 машин в день. (По очереди, каждый может пользоваться дорогой только один раз в 12 дней). Тогда все остальные машины распределятся равномерно по первоначальным участкам. Время в пути по первоначальному участку:

2,75 + 50 + 10 (2,75 + 0,5) = 85,25

В то же время, время в пути по привилегированному участку составит

10 (2,75 + 0,5) + (0,5 +10) + 10 (2,75 + 0,5) = 75,5

То есть, пользуясь дорогой один раз в 12 дней, человек будет экономить почти 12 минут. В то же время, в обычный день он тратит на 2 минуты больше, чем обычно.

• Ввести тариф за пользование дороги (по сути квотирование, аналогично предыдущему пункту).

Задача 2

Петя и Вася решили испечь торт «Секрет дружбы». Мальчики заранее договариваются о составе торта, а затем каждый из ребят в тайне от другого должен положить в тесто по одному ингредиенту: либо ягоды, либо орехи, либо шоколад. Любимый торт Васи – «Ягодный», в нем нет ничего, кроме ягод. А Петя обожает торт «Лесной» – с ягодами и орехами. Вася же, наоборот, «Лесной» терпеть не может. Оба мальчика не любят, когда шоколад в торте сочетается с какими-либо другими продуктами (с ягодами или орехами). Ко всем остальным сочетаниям ингредиентов мальчики равнодушны. До чего в результате договорятся мальчики? Какой ингредиент положит каждый из них на самом деле?

Решение:

Рассмотрим действия Пети:

• Если Вася выберет ягоды, то наилучший вариант для Пети – выбрать орехи.
• Если Вася выберет орехи, то Пете лучше всего положить ягоды.
• Если Вася выберет шоколад, самый подходящий вариант для Пети – выбрать шоколад.

Рассмотрим действия Васи:

• Если Петя выберет ягоды, Васе лучше выбрать ягоды.
• Если Петя выберет орехи, Вася выберет орехи.
• Если Петя положит шоколад, Васе стоит выбрать также шоколад.

Заметим, что в любой ситуации, кроме «шоколад-шоколад», одному из мальчиков выгодно отклониться от договорённости таким образом, что ему от этого станет лучше, а другому – хуже. Тогда другой мальчик не согласится на такой договор.
Таким образом, единственная ситуация, в которой никому из них не выгодно отклониться от договорённости и есть та, о которой они договорятся.

Ответ: они договорятся о шоколадном торте, каждый положит шоколад.

Задача 3

Владимир Муравьев работает менеджером по продажам в автосалоне. Его зарплата состоит из фиксированного ежемесячного оклада 15 000 рублей и бонуса 3 000 рублей за продажу каждого автомобиля. Екатерина Муравьева работала учителем в школе, сейчас находится в декретном отпуске и собирается вернуться на работу через год. Зарплата Екатерины составляла 25 000 рублей, сейчас она получает ежемесячное пособие в размере 10 000 рублей.

Муравьевы подсчитали, что средний уровень текущих расходов на нужды их семьи составляет 32 000 рублей в месяц. Сейчас Муравьевы живут в однокомнатной квартире и хотели бы через три года улучшить свои жилищные условия. Владимир и Екатерина исходят из того, что для обмена квартиры на двухкомнатную потребуется доплата не менее полутора миллионов рублей. В данный момент у Муравьевых есть сбережения в размере 300 тысяч рублей, которые они планируют разместить на три года на непополняемый банковский депозит под 7% годовых с ежегодным начислением процентов (процент начисляется на полную сумму, с учётом прошлых начислений).

Посчитав свои доходы и расходы, Муравьевы пришли к выводу, что достижение поставленной цели зависит от того, как будут идти дела на работе Владимира. На подъеме рынка Владимиру удавалось продавать в месяц до 12 машин, однако сейчас объем продаж автомобилей снизился на 25%.

Если доходов от продажи автомобилей всё же не хватит, семье придется брать кредит на покупку квартиры. Предельная сумма кредита, которую готовы взять Муравьевы, составляет 300 000 рублей.

Рассчитайте, какое минимальное количество автомобилей в среднем в месяц должен продавать Владимир, чтобы семья смогла в установленный срок реализовать поставленную финансовую цель только за счет собственных средств. Как изменится минимальное количество проданных автомобилей, если Муравьевы возьмут кредит? Позволит ли это реализовать финансовую цель семьи в случае, если объем продаж автомобилей сохранится на текущем уровне?

Решение:

1. Фиксированный доход семьи за три года составит 15*36 + 10*12 + 25*24 = 1260 тыс. руб.
2. Совокупные расходы на текущие нужды составят 32*36 = 1152.
3. После покрытия текущих расходов остается сумма 108 тыс. руб. на накопление.
4. Банковский вклад с процентами к концу третьего года составит 300*(1,1)^3 = 399,3 тыс. руб.
5. Если не брать кредит, за три года за счет доходов от продажи машин нужно накопить не менее чем 1500 – 108 – 399,3 = 992,7 тыс. руб., то есть всего нужно продать не меньше 331 машины (992,7/3 = 330,9), или 9,20 машин в месяц.
6. Если семья возьмет кредит, за счет бонусов нужно накопить не менее чем 
992,7 – 300 = 692,7, то есть всего нужно продать не меньше 231 машины (692,7/3 = 230,9), или 6,42 машины в месяц.
7. Да, позволит.

Задача 4

Город Волгоград имеет очень необычную планировку. Он растянулся на 60 километров с севера на юг вдоль правого берега Волги. Ширина города не превышает 10 километров, а в самых узких местах город можно за несколько минут пройти пешком поперек. Вот он, настоящий линейный город! Для удобства обозначений будем считать самую северную точку Волгограда 0-ым километром, а самую южную – 60-ым.

Волгоградская область славится своим мягким козьим пухом из Урюпинска. Какая досада, что в этом городе нет ни одного специализированного магазина, продающего исключительно мягкий козий пух из Урюпинска. В городе планируется открыть 2 таких магазина.

Продукция этих магазинов пользовалась бы спросом. Известно, что спрос на неё распределен равномерно вдоль реки Волга, то есть если, к примеру, в магазин станут ходить потенциальные покупатели, живущие в районе города с 0-ого по 12-ый километр, то это означает, что магазин удовлетворяет 20% спроса. Также известно, что пух из Урюпинска настолько качественный, что покупатели готовы и все 60 километров преодолеть, чтобы его заполучить, однако из двух магазинов они выберут ближайший. Если покупателям, проживающим по одному и тому же адресу, безразлично, в какой магазин идти, то одна половина из них пойдет в один магазин, а другая половина – в другой магазин.

1. Как нужно расположить магазины с точки зрения минимизации максимального расстояния, которое покупателю придется преодолеть на пути от дома до магазина? Дайте аргументированный ответ, выраженный в километрах от самой северной точки города.

Предположим теперь, что магазины принадлежат разным продавцам, конкурирующим за покупателей друг с другом. Цена на пух определяется поставщиком и не зависит от местоположения магазина.

2. Где разместит магазин первый владелец, если он точно знает, где расположен магазин второго владельца? Дайте ответ для всех возможных расположений второго магазина.

3. Где разместит магазин второй владелец, если он точно знает, где расположен магазин первого владельца? Дайте ответ для всех возможных расположений первого магазина.

4. Есть ли такое расположение магазинов, при котором каждому владельцу в отдельности не выгодно менять расположение своего магазина?

5. Эффективно ли такое расположение с точки зрения планировки города? Аргументируйте свой ответ.

Решение:

Будем обозначать расположение магазинов как и . Спрос на продукцию магазинов будем выражать в километрах и обозначать как Q1, Q2.

1) В этом пункте без ограничения общности перенумеруем магазины так, что X1 ≤ X2.

Всем потребителям, живущим севернее (X1 + X2)/2 км, ближе идти до магазина 1, а всем, живущим южнее, – до магазина 2.
Наиболее удаленный от магазинов покупатель может жить либо на окраине города (0 км, 60 км), либо ровно между магазинами ((X1 + X2)/2 км). Таким образом, расстояние может быть равно X1, 60 – X2 или (X1 + X2)/2 – X1 = (X2 – X1)/2. Опционально, здесь можно нарисовать график временных затрат для потребителя в зависимости от его места жительства.
Соответственно нам нужно минимизировать следующее выражение:

Минимум достигается там, где

Ответ:

2) Выразим функции спроса на магазин 1 в зависимости от и X1 и X2:

Предположим, что X2 < 30. Тогда, строго говоря, функция не достигает своего максимума, но наиболее выгодные для 1 магазина расположения находятся рядом с магазином 2, немного к югу от него.

Предположим, что X2 > 30. Тогда, строго говоря, функция не достигает своего максимума, но наиболее выгодные для 1 магазина расположения рядом с магазином 2, немного к северу от него.
Предположим, что X2 = 30. Тогда, максимум функции достигается в точке X1 = X2.

3) Аналогично пункту 2 (Допускается именно такая фраза в решении).

4) Если X1 < 30, то второму магазину выгодно быть рядом с магазином 1 (X2 < 30), но немного к югу. В таком случае 1 магазину выгодно отклониться и переместиться немного к югу от магазина 2.
Аналогично для случая X1 > 30.
В случае X1 = 30, оптимальный ответ: X2 = 30. В таком расположении никому не выгодно отклоняться и потому это равновесие.

5) Нет, не эффективно. При таком расположении наибольшее расстояние до магазина составит 30, в то время как при эффективном раскладе расстояние составит 15.