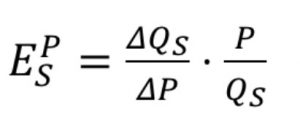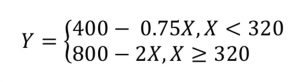Задания ОЧ-2016: 10 класс индивидуальный тур

Для решения экономических задач необходимы не только логика и знание алгебры, но и  умение применять экономические формулы и модели.

Задания индивидуального этапа для 10 класса — отличная возможность вспомнить базовые экономические понятия и формулы.

---

Задача 1

На рынке совершенной конкуренции в стране Ботанляндия спрос студентов на учебники имеет вид 
, где Q – величина спроса в штуках, а p – цена учебника в рублях.

Король страны решил нажиться на бедных школьниках и студентах и ввести налог в виде процента от цены покупателя (акциз).

До введения налога эластичность спроса в точке равновесия равнялась (-9/11), эластичность предложения (функция которого является линейной) до введения налога по абсолютной величине превышала эластичность спроса в 50t раз, где t – величина введенного позднее акциза (0<t<1).

После введения акциза (t) эластичность предложения стала равна 88/9, а равновесный объем упал на 4 единицы.

1. Сколько денег собрал король с помощью налога?

2. Может ли король изменить каким-либо образом налоговую ставку так, чтобы увеличить сборы?

Эластичностью спроса по цене называется следующая величина:  

аналогично эластичность предложения равна:

.

Решение: 

1.
Эластичность спроса вычисляется по формуле (допускается также поиск через т.н. геометрический смысл эластичности):
.
Откуда p = 90, Q = 22.

Тогда p′ = 110, Q′ = 18.

Функция предложения линейна. Обозначим её как .

В исходной точке эластичность .

В полученной точке  . (Подставляем цену для продавцов.)

Откуда b = 2, t = 0,2.

Тогда налогов король собрал следующую сумму:

T = t · p · Q = 0,2 · 110 · 18 = 396.

2.
Может. В качестве обоснования можно привести любой подходящий пример с обоснованием.

Функция предложения (находится из вышеуказанных уравнений): .

Функция спроса: .

Пусть он, например, введет потоварный налог в размере 60,5 единиц (или акцизный в размере 60,5/145 ) – соответствует наибольшему налоговому сбору. Тогда Q* = 11.

Налоговые сборы равны 665,5.

В качестве ответа годится любой иной обоснованный пример, показывающий, что ставка не является оптимальной.

Задача 2

В некотором государстве есть три города: Альфа (α), Бета (β), Дзета (ζ). В каждом из городов есть аэропорт. Города Альфа (α) и Бета (β), а также Бета (β) и Дзета (ζ) имеют прямое регулярное авиасообщение. Прямого авиасообщения между городами между Альфа (α) и Дзета (ζ) нет.

На рынке присутствует единственная авиакомпания OpenChampionshipAirways. На рейсах между Альфа (α) и Бета (β) используется самолет А320 с 158 местами.

На рейсах между городами Бета (β) и Дзета (ζ) используется самолет B747 вместимостью 505 пассажиров.

Издержки авиакомпании устроены так: на каждый рейс она тратит фиксированную сумму денег. За 1 совершенный рейс по указанному маршруту на A320 её издержки составляют 5000 дублонов. Аналогичные издержки для B747 составляют 15000 дублонов.

Авиакомпания продает билеты из Альфа (α) в Бета (β) и из Бета (β) в Дзета (ζ).

Устанавливая цены на авиабилеты, менеджмент авиакомпании располагал следующей информацией: P – установленная цена на перелет, Q – количество проданных билетов.

Спрос на перелет из Альфа (α) в Бета (β) описывается уравнением Q = 200 – P.
Спрос на перелет из Бета (β) в Дзета (ζ) описывается уравнением Q = 800 – 2P.

Когда число проданных билетов достигает числа мест в самолете, продажа заканчивается.

1. Какие цены установил менеджмент, исходя из располагаемой информации?

2. Некий аналитик заметил, что из-за того, что между Альфа (α) и Дзета (ζ) нет прямых рейсов, пассажиры готовы летать транзитом через Бета (β) и покупать два билета.
Спрос на такие билеты описывается уравнением Q = 100 – 1/3P, где P – цена в дублонах за весь маршрут, и не был учтён в оценках менеджмента (в т.ч. не входил в функции спроса из условия).
Какую прибыль на самом деле получила авиакомпания, если менеджмент установил цены, которые вы нашли в пункте 1?

3. Узнав о спросе на транзитные билеты из Альфа(α) в Дзета(ζ) менеджмент решил сделать специальную цену для такой категории пассажиров. Какие будут установлены цены на все три направления? (Предполагается, что по билету проданному для перелета из Альфа(α) в Дзета(ζ) невозможно пролететь только часть пути.) Прокомментируйте полученный результат. Чем можно объяснить полученные цены на билеты?

4. Менеджмент взял на стажировку студента. Студент должен был провести проверку и установить, какие расходы есть у авиакомпании. Выяснилось, что основные расходы делятся на следующие сегменты:

• Аэронавигация, аэропортовые сборы, наземное обслуживание
• Расходы на оплату труда экипажа
• Авиакеросин

Используя общие знания и жизненный опыт, помогите стажеру расположить затраты авиакомпании в порядке убывания (начиная с наиболее значимых и заканчивая наименьшими) и поясните ваши рассуждения.

 

Решение:

1.
У нас фиксированные издержки. Поэтому цены выбираем, исходя из идеи максимизации выручки на каждом участке.

Тогда для рейса из Альфа (α) в Бета (β):
 TR = (200 – P)P = 200P – P² => P* = 100, Q* = 100 < 158 – все поместятся в самолет.

Аналогично для рейса из Бета (β) в Дзета (ζ) TR = (800 – 2P)P = 800P – 2P² => P* = 200, Q* = 400 < 505 – все поместятся в самолет.
P* = 100, P* = 200.

2.
Получается, что для новой группы потребителей билет стоил 300 дублонов. За такую цену они покупают 0 билетов, поэтому Авиакомпания получила прибыль только от продажи билетов, найденных в п.1:

PR = (100 · 100 – 5000) + (200 · 400 – 15000) = 5000 + 65000 = 70000.

3.
Аналогично пунктам выше, мы максимизруем выручку.

Поэтому по возможности мы будем устанавливать цену, максимизируя выручку для этой группы пассажиров.

TRдоп. = (100 – 1/3P) · P = 100P – 1/3P² => P* = 150 => Q* = 50.

50 пассажиров запросто поместятся в самолеты обоих рейсов, поэтому мы установим такую цену. Наша прибыль будет увеличится на эту выручку. Таким образом:

PR = 70000 + 50 · 150 = 77500.

Цена на более длинный перелет с использованием того же рейса выходит дешевле, чем просто отдельный рейс. Объясняется ценовой дискриминацией: менее платежноспособным пассажирам из Альфа мы даем возможность путешествовать дешевле.

4.
1. а) Авиакеросин
1. б) Аэропортовые сборы, наземное обслуживание, аэронавигация
2. в) Расходы на оплату труда экипажа

Задача 3

В стране Омега продаются подержанные автомобили. Они бывают двух типов: в хорошем состоянии и в плохом состоянии.

Машины в хорошем состоянии, прослужат долго. Каждый продавец готов продать машину в хорошем состоянии не менее чем за 10 тыс. койнов. Покупатели готовы заплатить за хорошую машину не более 12 тыс. койнов.

Также на рынке продаются автомобили в плохом состоянии, которые в скором времени потребуют дорогостоящего ремонта. Каждый продавец готов продать автомобиль в плохом состоянии за 2 тыс. койнов, а покупатель готов купить такой автомобиль за 4 тыс. койнов.

Известно также, что в настоящее время половина продаваемых на рынке автомобилей имеют хорошее качество, а другая половина – плохое.

0. Каким цитрусовым в США называют подержанные автомобили плохого качества?

1. Пусть для начала и продавцы, и покупатели, знают о том, какой продаваемый автомобиль какого качества. По какой цене будут продаваться автомобили каждого вида? Если существует несколько возможных уровней цен, укажите их все.

2. Теперь пусть ни продавцы, ни покупатели не знают ничего о качестве автомобиля. По какой цене будут продаваться автомобили? Если существует несколько возможных уровней цен, укажите их все.

3. Наконец, рассмотрим ситуацию, в которой продавец знает, в каком состоянии его автомобиль. К примеру, он знает, что 10 лет назад машина побывала на дне реки. Покупатель же не может определить, какого качества автомобиль. Какие автомобили будут продаваться и по какой цене? Если существует несколько возможных уровней цен, укажите их все.

Примечание: покупатели и продавцы знают всегда о том, за сколько кто готов продать или купить автомобиль каждого состояния (и доли автомобилей в хорошем и плохом состоянии на рынке).
Если же есть неопределенность, какого качества автомобиль, то его оценивают с помощью математического ожидания. Математическим ожиданием мы называем следующую величину: M(H) = p1 · S1 + p2 · S2, где S1, S2 – значения субъективных оценок автомобилей, а p1, p2 – вероятность попадания того или иного автомобиля. (Подсказка: в данном случае p1 = p2 = 0,5.)

Решение:

0. Лимон, по статье Рынок «лимонов»: неопределенность качества и рыночный механизм (George A. Akerlof. The Market for «Lemons»: Quality Uncertainty and the Market Mechanism // The Quarterly Journal of Economics, v.84, August 1970, p. 488—500).

1. Хорошие: p ⊂ [10;12], плохие: p ⊂ [2;4].

2. Если никто не знает о качестве автомобиля, то покупатели готовы купить автомобиль по цене (4+12)/2=8, а продавцы готовы продать по цене (2+10)/2=6. Таким образом цена будет в промежутке [6;8].

3. Если на рынке продаются только плохие автомобили, то установится цена p ⊂ [2;4].

Если на рынке установится цена ≥ 10, то все автомобили будут продаваться по этой цене, потому что покупатели не отличают плохой автомобиль от хорошего.

Однако покупатели, не зная о качестве будут готовы заплатить максимум 8 (см предыдущий пункт).

Однако при цене p ≤ 8. Хорошие автомобили продаваться не будут, потому что производители готовы продавать их минимум по 10 тыс. койнов.

Хорошие автомобили продаваться не будут, таким образом на рынке будут продаваться только плохие автомобили, поэтому цена будет лежать в промежутке p ⊂ [2;4].

 

Задача 4

Крестьянин Иван владеет двумя полями площадью по 20 гектар. На одном гектаре первого поля можно вырастить 12 тонн пшена или 16 тонн ржи. На гектаре другого поля можно вырастить 8 тонн пшена или 4 тонны ржи. Известно, что Иван выращивает X0 тонн ржи и использует свои земельные ресурсы полностью и эффективно.

Старший брат Ивана владеет одним полем площадью в 40 гектар, на гектаре которого можно выращивать A тонн пшена или A тонн ржи, и предлагает Ивану обменяться злаковыми культурами.

Известно, что Иван согласится на обмен, если он сможет производить больше (по сравнению с ситуацией до обмена) хотя бы одной из культур и во всяком случае не меньше другой. При каких значениях A и X0 Иван согласится на обмен?

 

Решение:

Нетрудно заметить, что при A ≤ 10 Иван не согласится на обмен. В этом случае производственные возможности универсального поля полностью содержатся в производственных возможностях полей Ивана.

Также ясно, что при A > 12 Иван всегда будет соглашаться на сделку. Решается указанием на то, что в таком случае производственные возможности Ивана полностью содержатся в производственных возможностях его брата.

Найдем прямые, которые задают КПВ Ивана:

Куда включать точку излома не имеет значения.

Найдем прямую, характеризующую КПВ универсального поля:

Y = 40A – X

Найдем пересечение кривых производственных возможностей:

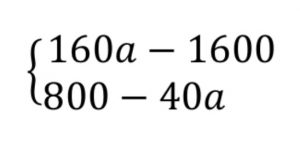
Иван будет соглашаться на обмен в тех точках, где КПВ универсального поля лежит выше КПВ Ивана, то есть:

Ответ